
BFS, DFS 두가지 모두 그래프를 탐색하는 방법입니다.
그래프란, 정점(node)과 그 정점을 연결하는 간선(edge)으로 이루어진 자료구조의 일종을 말하며,
그래프 탐색은 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것을 말합니다.
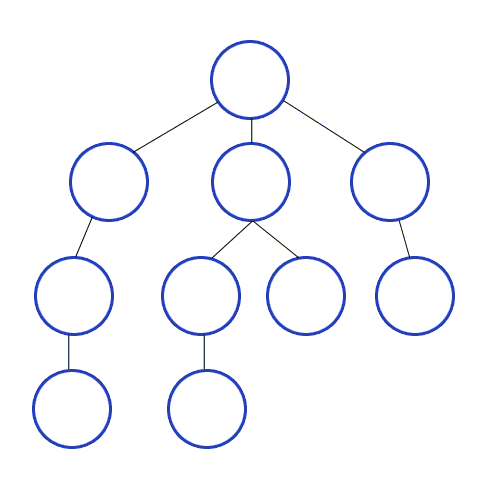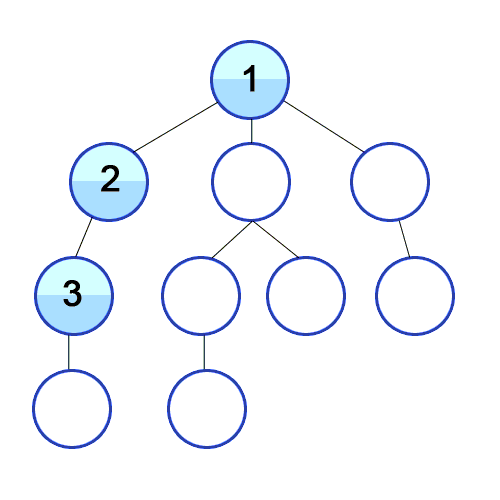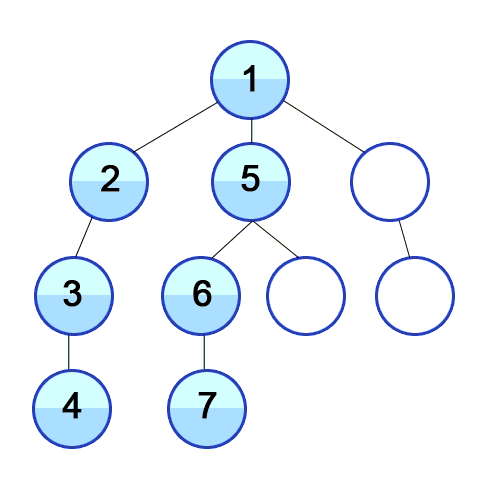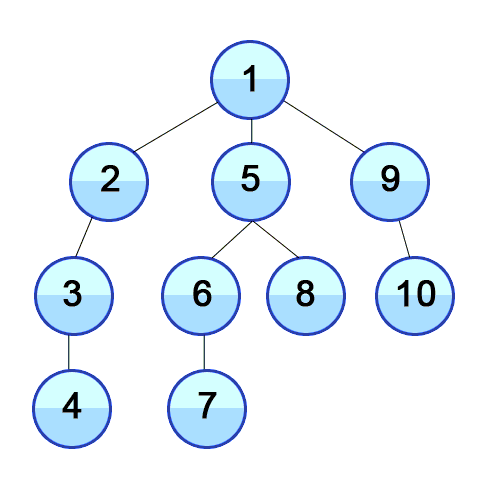
DFS 깊이 우선 탐색 (Depth-First Search)
출처 https://developer-mac.tistory.com/64
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식을 말합니다.
예를 들어, 미로찾기를 할 때 최대한 한 방향으로 갈 수 있을 때까지 쭉 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 그 갈림길부터 다시 다른 방향으로 탐색을 진행하는 것이 깊이 우선 탐색 방식이라고 할 수 있습니다.
BFS 너비 우선 탐색 (Breadth-First Search)
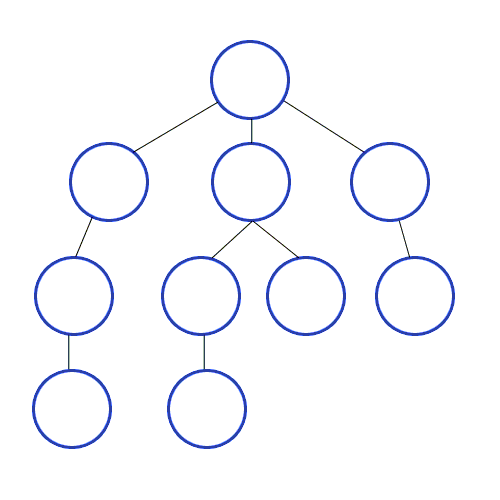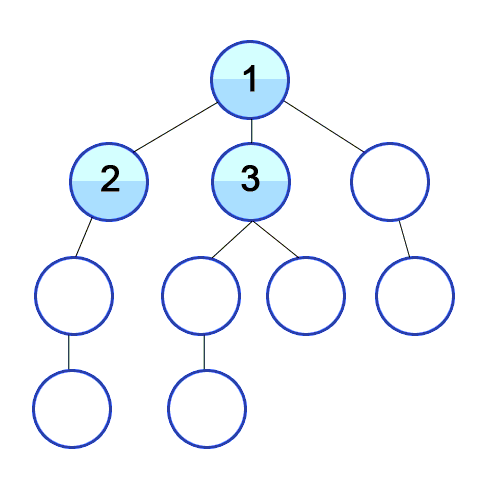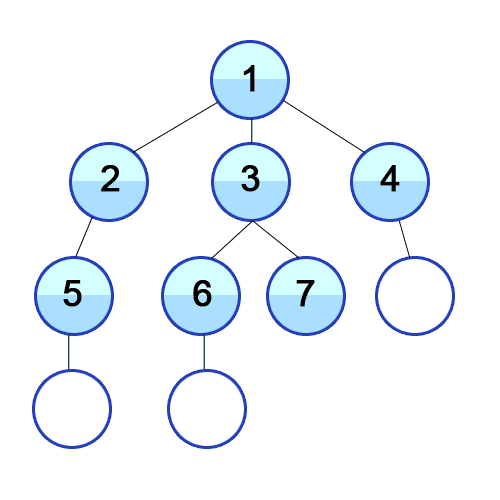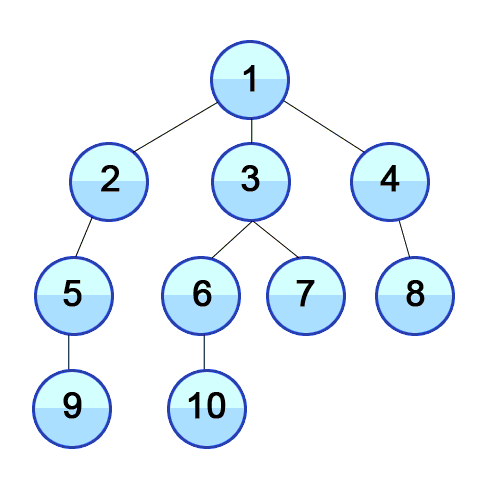
출처 https://developer-mac.tistory.com/64
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법으로,
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택합니다.
LeetCode: Max Area of Island
var maxAreaOfIsland = function(grid) {
//n, m은 가로세로 길이
let n = grid.length
let m = grid[0].length
let answer = 0
function DFS(x, y) {
//그래프의 범위를 벗어나면 false를 리턴
if (x < 0 || y < 0 || x >= n || y >= m) {
return 0;
}
//현재 요소가 1이면 0으로 바꿔서 방문 처리하고 상하좌우를 탐색
if (grid[x][y] === 1) {
grid[x][y] = 0;
return 1 + DFS(x - 1, y) + DFS(x, y - 1) + DFS(x + 1, y) + DFS(x, y + 1);
}
return 0;
}
//모든 요소를 확인하면서 true일 때 DFS함수 돌리기
//true일 때만, 즉 현재 요소가 0일 때만 answer에 1 더해주기
//true가 아니면 새로운 반복문으로 들어가므로 다른 섬을 탐색하게 됨
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (grid[i][j]) answer = Math.max(answer, DFS(i,j))
}
}
return answer;
};
이코테: 미로 탈출
const dir = [
[0, 1],
[0, -1],
[1, 0],
[-1, 0],
];
function solution(n, m, graph) {
//sx, sy: 시작점의 좌표
const bfs = (graph, sx, sy) => {
const q = [];
//큐에 현재 노드 넣어주기
q.push([sx, sy]);
//큐의 앞에서부터 요소를 꺼낸다
//큐에 들어있는 요소는 네번 돌 때 1이 되는 경우의 수
while (q.length !== 0) {
const [x, y] = q.shift();
console.log(`x, y: ${[x, y]}`);
//상하좌우 탐색
//nx, ny: 다음 탐색 좌표
for (let i = 0; i < 4; i++) {
//x,y에 각각 (0,1),(0,-1),(1,0),(-1,0)더하게 됨
const nx = x + dir[i][0];
const ny = y + dir[i][1];
//그래프를 벗어나면 다음 반복문을 실행
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
// 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if (graph[nx][ny] === 1) {
console.log(`nx, ny: ${[nx, ny]}`);
q.push([nx, ny]);
console.log(`q: ${q}`);
//그래프의 현재 요소를 지금까지의 길이로 교체
graph[nx][ny] = graph[x][y] + 1;
console.log(`graph: ${graph}`);
}
}
}
};
bfs(graph, 0, 0);
//지금까지의 길이를 리턴
return graph[n - 1][m - 1];
}
프로그래머스: 타겟 넘버
function solution(numbers, target) {
//모든 경우의 수를 탐색
//하나의 요소마다 두개의 경우의 수: 트리 구조
let answer = 0;
const l = numbers.length;
//DFS 함수는 재귀함수 실행 횟수와 지금까지의 합계를 인자로 받는다.
function DFS(n, sum) {
if (n === l) {
//탈출 조건: 재귀함수 실행 횟수가 배열 길이와 같아져 트리의 끝까지 탐색한 경우
//합이 타겟 넘버와 같아지면 답에 +1하고 리턴해서 종료
if(sum === target) answer ++;
return;
}
//재귀함수를 호출하면서 횟수를 1회 증가시키고 빼는 경우와 더하는 경우를 탐색
DFS(n+1, sum + numbers[n])
DFS(n+1, sum - numbers[n])
}
//DFS함수 실행
DFS(0, 0)
return answer;
}
프로그래머스: 게임 맵 최단거리
function solution(maps) {
//미리 경로 지정
const dir = [[1,0], [-1,0], [0,1], [0,-1]]
//가로 길이와 세로 길이: 벗어나지 않도록
const n = maps.length
const m = maps[0].length
//sx, sy는 스타트 지점을 의미: 끝에서 0,0으로 호출
function BFS(sx, sy){
//큐를 선언하고 일단 스타트 지점에서 시작
const q = []
q.push([sx, sy])
//더이상 갈 곳이 없으면 while 순회를 종료
while(q.length !== 0){
//큐에서 꺼낸 지점을 현재 지점으로 삼고
const [x, y] = q.shift();
//상하좌우로 다음 지점을 탐색한다. for loop을 총 네번 순회
for(let i=0; i<4; i++){
const nx = x+dir[i][0]
const ny = y+dir[i][1]
//맵을 벗어나면 다음 순회
if(nx<0||ny<0||nx>=n||ny>m) continue;
//다음 지점의 숫자가 1이라면(갈 수 있는 길이면) 큐에 다음 지점을 넣는다
if(maps[nx][ny] === 1){
q.push([nx,ny])
//해당 지점의 숫자를 지금까지 이동한 거리로 교체해 준다.
maps[nx][ny] = maps[x][y] + 1
}
}
}
}
//0,0에서 시작
BFS(0, 0)
/* 마지막 지점의 숫자가 1이라면(즉 한번도 도달한 적 없다면) -1을 리턴,
아니라면 그 지점에 도달하기까지 이동한 거리를 리턴 */
return maps[n-1][m-1] === 1 ? -1 : maps[n-1][m-1]
}'알고리즘' 카테고리의 다른 글
| 프로그래머스 lv.2 전력망을 둘로 나누기 (1) | 2023.05.02 |
|---|---|
| 완전탐색 (0) | 2023.04.25 |
| [자료구조] 스택/큐 (0) | 2023.04.04 |
| 내 즙을 짜낸 Greatest Common Divisor of Strings (0) | 2023.03.29 |
| 그리디 알고리즘(탐욕법) (2) | 2023.03.21 |
